Τι καθορίζει το μακροπρόθεσμο επιτρεπόμενο ρεύμα καλωδίου

Τι καθορίζει το μακροπρόθεσμο επιτρεπόμενο ρεύμα καλωδίου; Για να απαντήσουμε σε αυτή την ερώτηση, θα πρέπει να λάβουμε υπόψη τις παροδικές θερμικές διεργασίες που συμβαίνουν υπό συνθήκες όταν ένα ηλεκτρικό ρεύμα ρέει μέσω του αγωγού. Η θέρμανση και η ψύξη ενός αγωγού, η θερμοκρασία του, η σύνδεση με την αντίσταση και η διατομή - όλα αυτά θα αποτελέσουν αντικείμενο αυτού του άρθρου.

Διαδικασία μετάβασης

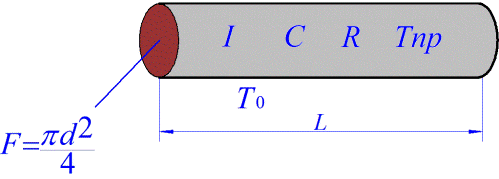
Αρχικά, θεωρήστε έναν συμβατικό κυλινδρικό αγωγό μήκους L, διάμετρο d, επιφάνεια διατομής F, αντίσταση R, όγκο V, προφανώς ίσο με το F * L, μέσω του οποίου ρέει το ρεύμα Ι, τη συγκεκριμένη θερμότητα του μετάλλου του οποίου κατασκευάζεται ο αγωγός - C, η μάζα του αγωγού ισούται με

m = V * Ω,

όπου Ω είναι η πυκνότητα του μετάλλου του αγωγού, S = pi * d * L είναι η περιοχή του πλευρικού τοιχώματος μέσω του οποίου συμβαίνει ψύξη, Tpr είναι η τρέχουσα θερμοκρασία του αγωγού, T0 είναι η θερμοκρασία περιβάλλοντος και συνεπώς T = Tpr - T0 είναι η μεταβολή της θερμοκρασίας. Ο ΚΤΡ είναι ο συντελεστής μεταφοράς θερμότητας, ο οποίος αριθμητικά χαρακτηρίζει την ποσότητα θερμότητας που μεταφέρεται από την επιφάνεια μονάδας ενός αγωγού σε 1 δευτερόλεπτο σε διαφορά θερμοκρασίας 1 βαθμού.

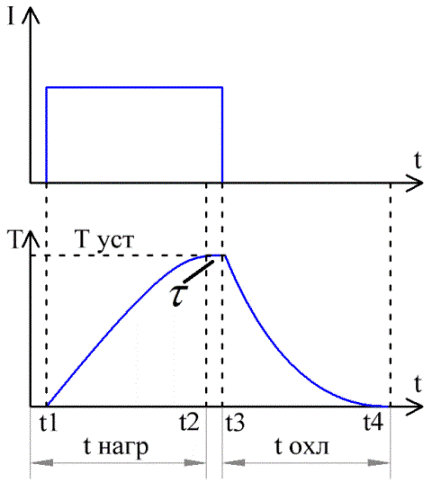
Το σχήμα δείχνει τα διαγράμματα του ρεύματος και της θερμοκρασίας στον αγωγό με την πάροδο του χρόνου. Από το χρόνο t1 έως το χρόνο t3, το ρεύμα I έπεσε μέσω του αγωγού.

Εδώ μπορείτε να δείτε πώς, μετά την ενεργοποίηση του ρεύματος, η θερμοκρασία του αγωγού αυξάνεται σταδιακά και στο χρόνο t2 παύει να αυξάνεται, σταθεροποιείται. Αλλά αφού σβήσουμε το ρεύμα στο χρόνο t3, η θερμοκρασία αρχίζει να μειώνεται σταδιακά και στο χρόνο t4 καθίσταται και πάλι ίσο με την αρχική τιμή (T0).

Έτσι, είναι δυνατόν να καταγράψουμε την εξίσωση ισορροπίας θερμότητας, μια διαφορική εξίσωση για τη διαδικασία θέρμανσης του αγωγού, όπου θα αντανακλάται ότι η θερμότητα που απελευθερώνεται στον αγωγό απορροφάται εν μέρει από τον ίδιο τον αγωγό και εν μέρει δίνεται στο περιβάλλον. Εδώ είναι η εξίσωση:

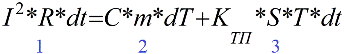
Στην αριστερή πλευρά της εξίσωσης (1) είναι η ποσότητα θερμότητας που απελευθερώνεται στον αγωγό κατά τη διάρκεια του χρόνου dt, η διέλευση του ρεύματος Ι.

Ο πρώτος όρος στη δεξιά πλευρά της εξίσωσης (2) είναι η ποσότητα θερμότητας που απορροφάται από το υλικό του αγωγού, από την οποία η θερμοκρασία του αγωγού αυξήθηκε κατά dT βαθμούς.

Ο δεύτερος όρος στη δεξιά πλευρά της εξίσωσης (3) είναι η ποσότητα θερμότητας που μεταφέρθηκε από τον αγωγό στο περιβάλλον κατά τη διάρκεια του χρόνου dt και σχετίζεται με την επιφάνεια του αγωγού S και τη διαφορά θερμοκρασίας T μέσω του συντελεστή θερμικής αγωγιμότητας Ktp.

Πρώτον, όταν το ρεύμα είναι ενεργοποιημένο, όλη η θερμότητα που απελευθερώνεται στον αγωγό χρησιμοποιείται για να θερμαίνει άμεσα τον αγωγό, πράγμα που οδηγεί σε αύξηση της θερμοκρασίας του, και αυτό οφείλεται στην θερμική χωρητικότητα C του υλικού αγωγού.

Με την αύξηση της θερμοκρασίας, η διαφορά θερμοκρασίας Τ μεταξύ του ίδιου του αγωγού και του περιβάλλοντος αυξάνεται αναλόγως και η παραγόμενη θερμότητα μερικώς πηγαίνει ήδη για να αυξηθεί η θερμοκρασία περιβάλλοντος.

Όταν η θερμοκρασία του αγωγού φθάσει σε μια σταθερή σταθερή τιμή Tust, αυτή τη στιγμή όλη η θερμότητα που απελευθερώνεται από την επιφάνεια του αγωγού μεταφέρεται στο περιβάλλον, έτσι ώστε η θερμοκρασία του αγωγού να μην αυξάνεται πλέον.

Η λύση στην εξίσωση διαφορικού θερμικού ισοζυγίου θα είναι:

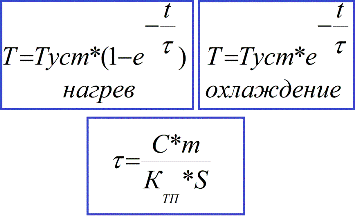
Στην πράξη, αυτή η μεταβατική διαδικασία δεν διαρκεί περισσότερο από τρεις σταθερές χρόνου (3 * τ), και μετά από αυτό το διάστημα η θερμοκρασία φτάνει το 0,95 * Tust. Όταν η διαδικασία μετάβασης θέρμανσης σταματήσει, η εξίσωση ισοζυγίου θερμότητας απλοποιείται και η σταθερή θερμοκρασία μπορεί να εκφραστεί εύκολα:

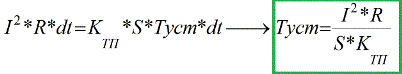
Επιτρεπτό ρεύμα

Τώρα μπορούμε να φτάσουμε σε τι ακριβώς αξία το ρεύμα φαίνεται να είναι ένα μακροπρόθεσμα αποδεκτό ρεύμα για έναν αγωγό ή ένα καλώδιο. Προφανώς, για κάθε αγωγό ή καλώδιο υπάρχει μια συγκεκριμένη κανονική συνεχής θερμοκρασία, σύμφωνα με την τεκμηρίωσή του.Αυτή είναι μια τέτοια θερμοκρασία στην οποία ένα καλώδιο ή ένα καλώδιο μπορεί να είναι συνεχώς και για μεγάλο χρονικό διάστημα χωρίς βλάβη στον εαυτό του και σε άλλους.

Από την παραπάνω εξίσωση καθίσταται σαφές ότι μια συγκεκριμένη τιμή ρεύματος συνδέεται με μια τέτοια θερμοκρασία. Αυτό το ρεύμα ονομάζεται επιτρεπόμενο ρεύμα καλωδίου. Αυτό είναι ένα τέτοιο ρεύμα, το οποίο, όταν διέρχεται από τον αγωγό για μεγάλο χρονικό διάστημα (περισσότερες από τρεις σταθερές χρόνου), το θερμαίνει σε μια επιτρεπόμενη, δηλαδή κανονική θερμοκρασία Tdd.

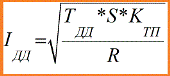
Εδώ: Idd - μακροπρόθεσμο επιτρεπόμενο ρεύμα αγωγού. TDD - επιτρεπτή θερμοκρασία αγωγού.

Για την επίλυση πρακτικών προβλημάτων, είναι πιο βολικό να προσδιορίσετε το μακροπρόθεσμο επιτρεπόμενο ρεύμα σύμφωνα με τους ειδικούς πίνακες του PUE.

Τύπος αγωγού

Επιτρεπτή θερμοκρασία

Βραχυπρόθεσμη επιτρεπτή θερμοκρασία

Έμπειρος αγωγός ή λεωφορείο

70^{περίπου}Με

Χαλκός - 300^{περίπου}Με

Έμπειρος αγωγός ή λεωφορείο

70^{περίπου}Με

Αλουμίνιο - 200^{περίπου}Με

Καλώδιο σε μόνωση χαρτιού μέχρι 3 kV

80^{περίπου}Με

200^{περίπου}Με

Καλώδιο σε μόνωση χαρτιού μέχρι 6 kV

65^{περίπου}Με

200^{περίπου}Με

Καλώδιο σε μόνωση χαρτιού μέχρι 10 kV

60^{περίπου}Με

200^{περίπου}Με

Καλώδιο σε μόνωση χαρτιού μέχρι 35 kV

50^{περίπου}Με

125^{περίπου}Με

Καλώδιο με λαστιχένια μόνωση μέχρι 1 kV

65^{περίπου}Με

150^{περίπου}Με

Καλώδιο σε μόνωση από PVC έως 1 kV

65^{περίπου}Με

150^{περίπου}Με

Καλώδιο μόνωσης XLPE έως 1 kV

90^{περίπου}Με

250^{περίπου}Με

Σε περίπτωση βραχυκυκλώματος, ένα σημαντικό ρεύμα βραχυκυκλώματος ρέει μέσω του αγωγού, το οποίο μπορεί να θερμαίνει σημαντικά τον αγωγό, υπερβαίνοντας την κανονική του θερμοκρασία. Για το λόγο αυτό, οι αγωγοί χαρακτηρίζονται από μια ελάχιστη διατομή που βασίζεται στην κατάσταση βραχυπρόθεσμης θέρμανσης του αγωγού από ένα ρεύμα βραχυκυκλώματος:

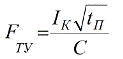
Εδώ: Ik - ρεύμα βραχυκυκλώματος σε αμπέρ; tp - μειωμένος χρόνος του ρεύματος βραχυκυκλώματος σε δευτερόλεπτα. Ο είναι ένας συντελεστής που εξαρτάται από το υλικό και την κατασκευή του αγωγού και από τη βραχυπρόθεσμη επιτρεπόμενη θερμοκρασία.

Ενότητα Σύνδεση

Τώρα ας δούμε πώς το μακροπρόθεσμα επιτρεπόμενο ρεύμα εξαρτάται από την διατομή του αγωγού. Έχοντας εκφράσει την περιοχή του πλευρικού τοιχώματος διαμέσου της διαμέτρου του αγωγού, θεωρώντας ότι η αντίσταση σχετίζεται με την περιοχή διατομής και την ειδική αντίσταση του υλικού του αγωγού και υποκαθιστώντας τον γνωστό τύπο αντίστασης στον τύπο Idd, που δίνεται παραπάνω, λαμβάνουμε για ένα τύπο μακροπρόθεσμου επιτρεπτού ρεύματος Idd :

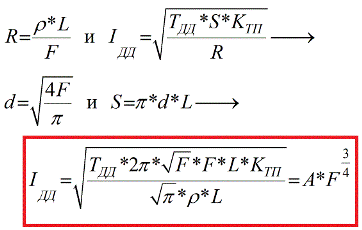
Είναι εύκολο να δούμε ότι η σύνδεση μεταξύ του μακροπρόθεσμου αποδεκτού ρεύματος του αγωγού Idd και της διατομής F δεν είναι άμεσα ανάλογη, εδώ η περιοχή της εγκάρσιας τομής ανυψώνεται στο ¾, πράγμα που σημαίνει ότι το μακροπρόθεσμα επιτρεπόμενο ρεύμα αυξάνεται πιο αργά από την διατομή του αγωγού. Άλλες σταθερές, όπως η αντίσταση, ο συντελεστής μεταφοράς θερμότητας, η επιτρεπτή θερμοκρασία, είναι ατομικές εξ ορισμού για κάθε αγωγό.

Στην πραγματικότητα, η εξάρτηση δεν μπορεί να είναι άμεση, επειδή όσο μεγαλύτερη είναι η διατομή του αγωγού, τόσο χειρότερα οι συνθήκες ψύξης των εσωτερικών στρωμάτων του αγωγού, η πιο αποδεκτή θερμοκρασία επιτυγχάνεται με χαμηλότερη πυκνότητα ρεύματος.

Εάν χρησιμοποιείτε αγωγούς μεγαλύτερης διατομής για να αποφύγετε την υπερθέρμανση, αυτό θα οδηγήσει σε υπερβολική κατανάλωση υλικού. Είναι πολύ πιο κερδοφόρο να χρησιμοποιείτε πολλούς αγωγούς μικρής διατομής τοποθετημένους παράλληλα, δηλαδή, να χρησιμοποιείτε πολυκονικούς αγωγούς ή καλώδια. Και η σχέση μεταξύ του μακροπρόθεσμου επιτρεπόμενου ρεύματος και της περιοχής της εγκάρσιας διατομής στο σύνολό της αποδεικνύεται ως εξής:

F

1

2

4

Εγώdd

1

1,68

2,83

Ρεύμα και θερμοκρασία

Για να υπολογίσετε τη θερμοκρασία ενός αγωγού με γνωστό ρεύμα και συγκεκριμένες εξωτερικές συνθήκες, σκεφτείτε τη σταθερή κατάσταση όταν η θερμοκρασία του αγωγού φτάσει στο Tust και δεν αυξάνεται πλέον. Αρχικά δεδομένα - ρεύμα Ι, συντελεστής μεταφοράς θερμότητας Ktp, αντίσταση R, περιοχή πλευρικών τοιχωμάτων S, θερμοκρασία περιβάλλοντος T0:

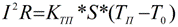
Ένας παρόμοιος υπολογισμός για συνεχές ρεύμα:

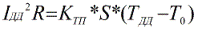
Εδώ, το T0 λαμβάνεται ως υπολογιζόμενη θερμοκρασία περιβάλλοντος, για παράδειγμα + 15 ° C για τοποθέτηση κάτω από το νερό και στο έδαφος, ή + 25 ° C για τοποθέτηση στον αέρα. Τα αποτελέσματα των υπολογισμών αυτών δίδονται στο πίνακες συνεχών ρευμάτων, και για τον αέρα παίρνουν θερμοκρασία + 25 ° C, επειδή αυτή είναι η μέση θερμοκρασία του καυτού μήνα.

Διαχωρίζοντας την πρώτη εξίσωση από το δεύτερο και εκφράζοντας τη θερμοκρασία του αγωγού, μπορούμε να λάβουμε μια φόρμουλα για την εύρεση της θερμοκρασίας του αγωγού σε ένα ρεύμα διαφορετικό από το μακροπρόθεσμα επιτρεπτό και σε δεδομένη θερμοκρασία περιβάλλοντος, εάν είναι γνωστό ένα μακροπρόθεσμα επιτρεπόμενο ρεύμα και μια μακροπρόθεσμα επιτρεπόμενη θερμοκρασία και δεν χρειάζεται να καταφύγετε στη χρήση άλλων σταθερές:

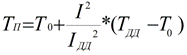
Από τον τύπο αυτό φαίνεται ότι η αύξηση της θερμοκρασίας είναι ανάλογη προς το τετράγωνο του ρεύματος και αν το ρεύμα αυξάνεται κατά 2 φορές τότε η αύξηση της θερμοκρασίας θα αυξηθεί κατά 4 φορές.

Εάν οι εξωτερικές συνθήκες διαφέρουν από τον σχεδιασμό

Ανάλογα με τις πραγματικές εξωτερικές συνθήκες, οι οποίες μπορεί να διαφέρουν από τις υπολογιζόμενες ανάλογα με τη μέθοδο τοποθέτησης, για παράδειγμα, αρκετούς αγωγούς (καλώδιο) που βρίσκονται παράλληλα ή τοποθετούνται στο έδαφος σε διαφορετική θερμοκρασία, απαιτείται ρύθμιση του μέγιστου επιτρεπτού ρεύματος.

Στη συνέχεια εισάγεται ο συντελεστής διόρθωσης Kt, με τον οποίο πολλαπλασιάζεται το μακροπρόθεσμα επιτρεπόμενο ρεύμα υπό γνωστές (πίνακες) συνθήκες. Εάν η εξωτερική θερμοκρασία είναι μικρότερη από την υπολογιζόμενη τιμή, τότε ο συντελεστής είναι μεγαλύτερος από έναν · αν είναι υψηλότερος από τον υπολογισμένο, τότε, το Kt είναι μικρότερο από ένα.

Όταν τοποθετούνται πολλοί παράλληλοι αγωγοί πολύ κοντά ο ένας στον άλλο, θα θερμαίνονται επιπλέον, αλλά μόνο εάν το περιβάλλον περιβάλλον είναι ακίνητο. Οι πραγματικές συνθήκες συχνά οδηγούν στο γεγονός ότι το περιβάλλον είναι κινητό (αέρας, νερό) και η μεταφορά προκαλεί την ψύξη των αγωγών.

Εάν το μέσο είναι σχεδόν ακίνητο, για παράδειγμα, όταν τοποθετείτε σε σωλήνα υπόγεια ή σε αγωγό, τότε η αμοιβαία θέρμανση θα προκαλέσει μείωση του μακροπρόθεσμου επιτρεπόμενου ρεύματος και εδώ θα πρέπει να εισαγάγετε και πάλι τον διορθωτικό συντελεστή Kn, ο οποίος δίνεται στην τεκμηρίωση καλωδίων και συρμάτων.

Comments

[#1]

Σε γενικές γραμμές, κάθε προμηθευτής συρμάτων ή καλωδίων που σέβεται τον εαυτό σας παρέχει σήμερα συνοδευτικούς πίνακες, όπου για ένα συγκεκριμένο καλώδιο σε διάφορες συνθήκες μπορείτε να βρείτε εύκολα ένα μακροπρόθεσμο επιτρεπόμενο ρεύμα και να μην κάνετε λάθος. Ο ίδιος ο κατασκευαστής πραγματοποιεί όλους τους απαραίτητους υπολογισμούς και υπολογισμούς και ο καταναλωτής μπορεί να επιλέξει από το τραπέζι ένα καλώδιο ή σύρμα κατάλληλου τμήματος και την απαιτούμενη τροποποίηση.

[#2 Anatoly]

Αλλά όχι μόνο όταν το καλώδιο τοποθετείται στο έδαφος αλλά και όταν το τοποθετείτε απευθείας στις πύλες κάτω από το γύψο, οι συνθήκες τοποθέτησης του καλωδίου ενδέχεται να διαφέρουν από τις υπολογιζόμενες (δυστυχώς, στα κανονιστικά και τεχνικά έγγραφα, συμπεριλαμβανομένου του PUE, δεν δίνεται η δέουσα προσοχή στο θέμα αυτό). Για παράδειγμα, σύμφωνα με το PUE, το ονομαστικό ρεύμα του καλωδίου κατά την τοποθέτησή του στον σωλήνα, και η πτυχή PVC είναι ουσιαστικά ένας εύκαμπτος σωλήνας από PVC, το ονομαστικό ρεύμα του καλωδίου, με συντελεστή πλήρωσης της αυλάκωσης με καλώδιο 0,3-0,5, είναι 21 amp; στην άμμο Εάν χρησιμοποιήσετε GOST RM EK 60287 - 2 - 1 - 2009, γνωρίζοντας ότι η θερμική αντίσταση του ασβεστοκονιάματος είναι κατά μέσο όρο 1 (m * βαθμός Κελσίου / Watt) και η θερμική αντίσταση του πνεύμονα του αεριωμένου σκυροδέματος είναι ίσο με 10 (m * βαθμούς Κελσίου / Watt), προκύπτει ότι το ονομαστικό ρεύμα του ρεύματος καλωδίου στο αεριωμένο σκυρόδεμα είναι 20 * 20/10 = 40, εκχυλίζουμε την τετραγωνική ρίζα και παίρνουμε περίπου 7.1 αμπέρ, η μία πλευρά είναι καλυμμένη με γύψο, το ονομαστικό ρεύμα του καλωδίου είναι περίπου 10 ίντσες, δύο φορές Αν το καλώδιο εκτείνεται σε ένα εκτεταμένο τμήμα αερισμένου σκυροδέματος, γύψου κ.λπ., σύμφωνα με το PUE, το ονομαστικό ρεύμα του καλωδίου πρέπει να επιλέγεται σύμφωνα με τις χειρότερες συνθήκες τοποθέτησης ή ρεύματος στα 10 amperes και έναν αυτόματο διακόπτη 6 amp Cayuel. ΑΛΛΑ, εάν τοποθετήσετε το καλώδιο και επίσης το καλώδιο, έτσι ώστε το περίβλημα να μην εμποδίζει την καλύτερη ψύξη του, τότε το ονομαστικό ρεύμα του καλωδίου είναι 21 αμπέρ, αφού το περιβάλλον τοποθέτησης του δεν έχει αλλάξει.Και η πρακτική της λειτουργίας επιβεβαιώνει ότι αυτό συμβαίνει, ο σημαντικότερος σκοπός της αυλακώσεως είναι η διατήρηση του ονομαστικού ρεύματος του καλωδίου ανεξαρτήτως των συνθηκών τοποθέτησής του, δηλαδή ανεξάρτητα από τη θερμική αντοχή των υλικών στα οποία έχει τοποθετηθεί το καλώδιο Η κυματοειδής αυλάκωση είναι ειδικά σχεδιασμένη για να ικανοποιεί αυτή την απαίτηση διατηρώντας το ονομαστικό ρεύμα του καλωδίου, η θερμική ενέργεια που απελευθερώνεται από το καλώδιο απορροφάται από τον αέρα στην αυλάκωση και το υλικό της αυλακώσεως το ίδιο με τη μεταφορά και την ακτινοβολία θερμότητας και η μεταφορά θερμότητας δεν παίζει σημαντικό ρόλο ο ρόλος της ψύξης του καλωδίου, λόγω της πολύ μεγάλης θερμικής αντίστασης του αέρα και της ίδιας της αυλακώσεως, βεβαίως, όταν τοποθετείται σε υλικά με χαμηλή θερμική αντίσταση, η θερμοκρασία της αυλάκωσης μειώνεται και είναι ικανή να απορροφήσει περισσότερη θερμική ενέργεια, αλλά αυτή η μείωση δεν είναι σημαντική. , η θερμική αντίσταση του αεριωμένου σκυροδέματος δεν είναι μεγαλύτερη από 18 - 20% της θερμικής αντίστασης του αέρα στην αυλάκωση, δηλαδή ακόμη και με μια απείρως μεγάλη αντίσταση του εξωτερικού περιβάλλοντος τοποθέτησης της αυλάκωσης, το καλώδιο στο ονομαστικό ρεύμα δεν θερμαίνεται Η θερμοκρασία θα είναι υψηλότερη από την επιτρεπόμενη θερμοκρασία και σε ένα περιβάλλον με χαμηλή θερμική αντίσταση το καλώδιο θα έχει θερμοκρασία όταν το τοποθετεί στην αυλάκωση ακόμα χαμηλότερα από το μέγιστο επιτρεπτό.Η αυλάκωση δημιουργήθηκε αντί των χαλύβδινων σωλήνων όταν διάφορα υλικά με διαφορετική θερμική αντίσταση κατά μήκος των διαδρομών τοποθέτησης των καλωδίων άρχισαν να χρησιμοποιούνται στην κατασκευή .

[#3 Νικολάι]

Οποιοδήποτε συνεχώς ρέον ρεύμα υπό σταθερές εξωτερικές συνθήκες αντιστοιχεί σε μια καλά καθορισμένη σταθερή θερμοκρασία του αγωγού. Το μέγεθος του μακροχρόνιου ρεύματος στο οποίο η θερμοκρασία καθίσταται το μέγιστο επιτρεπτό για μια δεδομένη μάρκα σύρματος ή καλωδίου ονομάζεται μακροπρόθεσμο φορτίο ρεύματος.

Το μέγεθος του μακροπρόθεσμου επιτρεπόμενου ρεύματος εξαρτάται από το υλικό και τη διατομή του αγωγού, τη θερμοκρασία περιβάλλοντος, το μονωτικό υλικό και τη μέθοδο τοποθέτησης. Ο τρόπος λειτουργίας των καλωδίων και των καλωδίων έχει επίσης σημασία. Σε διακοπτόμενη λειτουργία, το επιτρεπτό φορτίο ρεύματος μπορεί να αυξηθεί. Για να προσδιοριστεί η τιμή του μακροπρόθεσμου επιτρεπτού ρεύματος, είναι σημαντικό να γνωρίζουμε την υψηλότερη θετική θερμοκρασία περιβάλλοντος, καθώς σε χαμηλές θερμοκρασίες στο ίδιο ρεύμα παρέχονται ευνοϊκότερες συνθήκες εργασίας των συρμάτων και των καλωδίων.

[#4 Alex]

Δεν είναι σαφές - όπως για ένα σύρμα με τετραγωνική διατομή 2 mm, η ισχύς του ρεύματος είναι μόνο 1,68 A ???

25Α μπορείτε εύκολα, δεν καταλαβαίνω τίποτα ...